• 
• 
• 

هاتف: +963-31-2220008
جوال: +963-999-824193
سوريا - حمص

مقدمة

سأعرض هنا أيضاً خوارزمية أخرى في مجال الرياضيات العددية يستخدمها المهندس المبرمج بكثرة في برامجه وهي خوارزمية حل جملة معادلات خطية، أي حل n معادلة خطية بـ n مجهول.

تستخدم هذه الخوارزمية في البرامج الإنشائية في طريقة الصلابة مثلاً، وفي مجالات أخرى.

هناك عدة خوارزميات لحل جملة المعادلات هذه، لكل واحدة ميزاتها الخاصة، وقد اخترت هنا طريقة الحذف لغوص لبساطتها، وهي تقوم بالمطلوب بشكل ممتاز.

فكرة عامة

لنفرض أنه لدينا جملة المعادلات التالية:

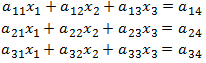
ونريد إيجاد قيم المجاهيل x₁ و x₂ و x₃

سنسمي المصفوفة التالية مصفوفة الأمثال:

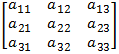
وسنسمي المصفوفة التالية مصفوفة الأمثال الموسعة:

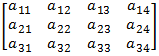
يوجد عدة طرق لحل جملة المعادلات هذه أو أي جملة معادلات خطية من الدرجة n، منها:

• إيجاد مقلوب مصفوفة الأمثال وضربه بشعاع الطرف الثاني، وقد استخدمتها في ملف الإكسل المشار إليه هنا.
• طريقة غوص وهي موضوع البحث
• طريقة غوص جوردان
• طريقة كولسكي
• طريقة غوص سايدل العددية
• طرق أخرى...

سنعتبر أثناء دراستنا أن جملة المعادلات الأصلية لها حل وحيد، ولكن أثناء عملية التحليل سنختبر إن كانت مصفوفة الأمثال نظامية أو شاذة، فإن كانت نظامية فعندها يوجد حل وحيد للجملة سنقوم بإيجاده، وإلا سنخرج من البرنامج مع رسالة خطأ تفيد أنه لا يوجد حل وحيد للجملة.

ملاحظة: نقول أن مصفوفة الأمثال شاذة إذا كان معينها (محددها) يساوي الصفر.

وقبل البدء سأذكّر بالتحويلات الأولية التي يمكننا تطبيقها على جملة المعادلات بحيث نحصل على جملة معادلات مكافئة، أي لها نفس الحل، وهذه التحويلات هي:

1. تبديل معادلتين: وهذا واضح أنه لا يغير الحل.
2. ضرب طرفي معادلة بعدد لا يساوي الصفر: إذا كان لدينا طرفان متساويان فإنه بضرب كل طرف بنفس العدد سنحصل أيضاً على طرفين متساويين.
3. إضافة معادلة مضروبة بعدد إلى معادلة ثانية: أيضاً إذا كان لدينا طرفان متساويان وأضفنا إلى كل طرف عدداً ما نحصل على طرفين متساويين.

مبدأ طريقة التحويلات لغوص

إن مبدأ الطريقة هو تحويل جملة المعادلات السابقة إلى جملة معادلات مكافئة بالشكل التالي:

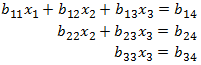
أي تحويل جملة المعادلات إلى شكل مثلثي يسهل معه حساب قيم المتحولات.

ففي جملة المعادلات المكافئة، من المعادلة الثالثة نحصل على x₃ بسهولة، ونعوضها في المعادلة الثانية لنحصل على x₂ ونعوض القيمتين في المعادلة الأولى لنحصل على x₁.

إجراء التحويلات

إذا قسمنا المعادلة الأولى من جملة المعادلات الأولى على a₁₁ (بفرض a₁₁ لا يساوي الصفر) وضربناها ب a₂₁ ثم طرحناها من المعادلة الثانية (أي طبقنا التحويل الثالث على المعادلة الثانية)، ونفس الشيء فعلناه مع المعادلة الثالثة أي قسمنا الأولى على a₁₁ وضربناها ب a₃₁ ثم طرحناها من الثالثة فإننا نحصل على جملة المعادلات المكافئة التالية:

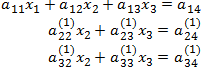
إن الرقم بين قوسين فوق الحد يدل على رقم عملية التحويل.

أي أننا بهذه العملية اختصرنا الحد الأول من المعادلتين الثانية والثالثة، وسنسمي الحد a₁₁ محور المعادلة رقم 1.

ويمكننا ترجمة ذلك بشكل رمزي كما يلي:

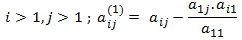
ولكن ماذا لو كان a₁₁=0؟

نقوم عندها بتبديل المعادلة الأولى مع أي من المعادلات التي تليها بحيث يكون الحد a_i1 لا يساوي الصفر حيث i هو رقم السطر.

فإن لم نجد، وكانت كلها تساوي الصفر؟

عندها نحكم أن مصفوفة الأمثال شاذة وليس لجملة المعادلات حل وحيد، والسبب أن إحدى المعادلات (أو أكثر) مرتبطة خطياً بمعادلات أخرى.

نعود إلى جملة المعادلات الأخيرة وسنحاول حذف a₃₂⁽¹⁾ الجديد من المعادلة الثالثة.

نكرر العملية بأن ننسى المعادلة الأولى وتصبح لدينا المعادلتان الثانية والثالثة بمجهولين، أي أننا نقسم المعادلة الثانية (الجديدة) على محورها وهو a₂₂⁽¹⁾ ونضربها ب a₃₂⁽¹⁾ ونجمعها إلى الثالثة فنحصل على جملة المعادلات المكافئة التالية:

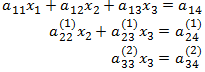
ونترجم ذلك بشكل رمزي كما يلي:

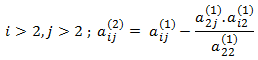
وهكذا حذفنا الحد الثاني أيضاً من المعادلة الثالثة.

الآن يمكننا حساب المجاهيل بسهولة كما يلي:

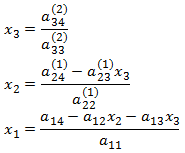
أي بشكل رمزي:

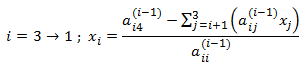
تعميم الحالة على n معادلة

إن عمليات التحويل تصبح بالشكل:

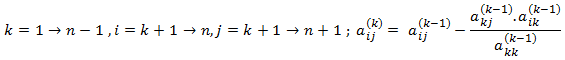
أي أنه لدينا ثلاث حلقات متداخلة:

1. الحلقة الأولى هي حلقة k وتبدأ من 1 وحتى n-1 وفيها نختار المحور a_kk
2. الحلقة الثانية وهي ضمن الأولى وهي حلقة i وتبدأ من السطر الذي يلي سطر المحور k، أي تبدأ من k+1 وتنتهي في السطر n، وهي تمثل السطر الذي سنقوم بعملية التحويل له.
3. الحلقة الثالثة وهي ضمن الثانية وهي حلقة j وتبدأ من رقم العمود الذي يلي رقم عمود المحور وهو k، أي تبدأ من k+1 وتنتهي في آخر عمود وهو n+1، على اعتبار أن كل العناصر في السطر i قبل العمود k+1 تساوي الصفر.

ملاحظة: فرضنا أن a_kk لا تساوي الصفر، فإن كانت كذلك نقوم بتبديل السطر k بسطر آخر يليه بحيث يكون a_kk الجديد لا يساوي الصفر، فإن لم يوجد قلنا أن جملة المعادلات لا تملك حلاً وحيداً، كما وضحنا ذلك سابقاً.

ملاحظة2: سيتم توضيح هذه الحلقات في البرنامج لاحقاً.

أما تفسير علاقة حساب a_ij فهي:

إن قيمة a_ij الجديدة تساوي قيمتها القديمة التي حصلنا عليها من الحساب السابق مطروحاً منها (قيمة a في نفس عمودها في سطر العنصر المحور مضروبة في قيمة a في نفس سطرها في عمود العنصر المحور ومقسومة على العنصر المحور) أي كما في الشكل:

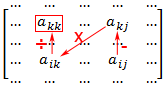
أما حساب x في الحالة العامة فهو بالشكل:

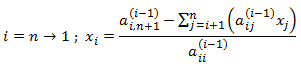
وهنا لدينا حلقتان متداخلتان:

1. الأولى هي حلقة i وتبدأ من n وتنتهي ب 1، وهي تدل على رقم المجهول المراد حساب قيمته.
2. حلقة ضمنها وهي حلقة j وهي تستخدم للجمع، وتبدأ من i+1 وتنتهي ب n

أرجو أن يكون الشرح واضحاً، وسيتوضح أكثر إن شاء الله عند حل مثال، وأكثر عند ترجمة الخوارزمية إلى برنامج حاسوبي كما سيأتي لاحقاً.

مثال يدوي

المطلوب حل جملة المعادلات التالية:

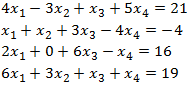
الحل:

نقوم أولاً بتشكيل مصفوفة الأمثال الموسعة:

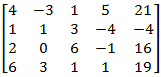
نجري التحويلات الأولى على اعتبار أن العنصر المحور هو العنصر في السطر والعمود الأول وهو الرقم 4.

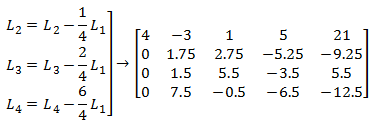
في الشكل السابق، الطرف الأيسر يدل على التحويلات التي قمنا بها، حيث L يدل على السطر.

قمنا في هذه التحويلات بحذف أمثال x₁ من جميع المعادلات التي تحت السطر رقم 1.

نلاحظ أن المحور هو العنصر الأول في السطر الأول وهو الرقم 4 والذي قمنا به أننا طرحنا من كل سطر (بعد سطر المحور)، طرحنا منه السطر الأول (سطر المحور) مقسوماً على المحور (الرقم 4) مضروباً بالعنصر الذي في نفس السطر الذي نريد إجراء التحويل عليه والموجود أيضاً في نفس عمود المحور.

فمثلاً العنصر في السطر الثاني والعمود الرابع من جملة المعادلات الأساسية وهو -4 ، نجري عليه التحويل المبين أعلاه كما يلي:

L₂ = L₂ - 1/4 * L₁ => -4 – 1/4 * 5 = -5.25

قد يبدو الكلام معقداً، ولكن بالعودة إلى الشكل السابق والنظر إلى التحويلات وبالتأكد يدوياً يمكن فهم الفكرة بسهولة.

نعيد نفس الكرة، ونحذف أمثال x₂ في المعادلات التي تلي المعادلة الثانية، وفي هذه الحالة نعتمد جملة المعادلات الأخيرة ويكون المحور هو العنصر الموجود في السطر الثاني والعمود الثاني وهو 1.75

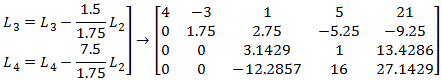
نعيد نفس الكرة، ونحذف أمثال x₃ في المعادلات التي تلي المعادلة الثالثة، وفي هذه الحالة نعتمد جملة المعادلات الأخيرة ويكون المحور هو العنصر الموجود في السطر الثالث والعمود الثالث وهو 3.1429

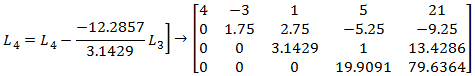
الآن فإن حل جملة المعادلات الأصلية هو نفسه حل جملة المعادلات الأخيرة المكافئة لها، ونبدأ بإيجاد x₄ ثم x₃ وهكذا:

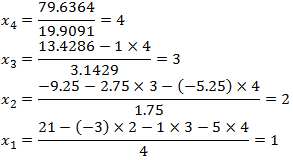
وهو الحل المطلوب، ويمكن التأكد بالتعويض في جملة المعادلات الأساسية أو أي جملة معادلات مكافئة.

تحويل الخوارزمية إلى برنامج بلغة Visual Basic 6

بعد أن قمنا بدراسة الخوارزمية السابقة يمكننا بسهولة تحويلها إلى أي لغة برمجة، وقد اخترت لغة Visual Basic لانتشارها الواسع أولاً، ولخبرتي فيها ثانياً!

وهنا سأستخدم لغة VBA المدمجة مع إكسل لوجودها على كل جهاز تقريباً...

وقبل البدء أنصح بشدة الرجوع إلى الدرسين الرابع والخامس من سلسلة دروس برمجة إكسل في هذا الموقع.

سنقوم أولاً بإنشاء تابع اسمه EquationsGauss، نمرر له مصفوفة الأمثال الموسعة، فيعيد لنا شعاع حل المعادلات، وفي حال كانت جملة المعادلات لا تملك حلاً وحيداً، سيقوم هذا التابع بإصدار خطأ.

نضيف العبارتين التاليتين لتعريف التابع:

Public Function EquationsGauss(A() As Double) As Double()

End Function

إن أي سطر نضيفه سيكون بين السطرين السابقين.

نلاحظ أننا قمنا بتمرير مصفوفة الأمثال الموسعة للبرنامج ومن المفيد أن نعلم عدد المعادلات.

نقوم أولاً بحجز متحول اسمه n سيدل على عدد المعادلات ثم سنستخدم التابع UBound الذي يعطينا الحد الأعلى للمصفوفة، كما يلي:

Dim n As Integer
'عدد المعادلات
n = UBound(A, 1)

ملاحظة: إن القيمة 1 في التابع السابق UBound تعني البعد الأول للمصفوفة وهو في حالتنا عدد الأسطر.

نريد الآن ترجمة العبارة الرمزية السابقة وهي:

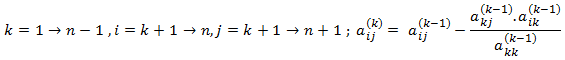
إلى برنامج، لذلك نقوم بتعريف المتحولات k,i,j ثم نضع الحلقات التي تم شرحها سابقاً، كما يلي:

'إجراء عمليات التحويل
Dim k As Integer, i As Integer, j As Integer
For k = 1 To n - 1
    For i = k + 1 To n
        For j = k+1 To n + 1
            A(i, j) = A(i, j) - A(k, j) * A(i, k) / A(k, k)
        Next
    Next
Next

ملاحظة: لم نقم هنا باختبار إن كانت قيمة a(k,k) تساوي الصفر وافترضناها لا تساوي الصفر، لتسهيل فهم البرنامج، وسنعالج هذا الأمر لاحقاً.

الآن سنقوم بحساب قيم المجاهيل كما في العبارة الرمزية السابقة وهي:

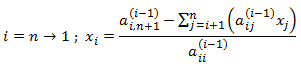
'حساب المجاهيل
ReDim x(n) As Double: Dim s As Double
For i = n To 1 Step -1
    s = 0
    For j = i + 1 To n
        s = s + A(i, j) * x(j)
    Next
    x(i) = (A(i, n + 1) - s) / A(i, i)
Next
EquationsGauss = x

نلاحظ أننا عرفنا متحولاً s من أجل حساب المجموع المبين في المعادلة، ويجب دائماً أن نجعل قيمته صفراً قبل حلقة j حتى لا يحتفظ بقيمته السابقة.

في نهاية البرنامج قمنا بإسناد قيمة x إلى EquationsGauss وهو اسم التابع، وهي خطوة ضرورية ليعلم التابع أي قيمة سيعيد.

يصبح البرنامج كله حتى هذه النقطة:

Public Function EquationsGauss(A() As Double) As Double()
    Dim n As Integer
    'عدد المعادلات
    n = UBound(A, 1)

    'إجراء عمليات التحويل
    Dim k As Integer, i As Integer, j As Integer
    For k = 1 To n - 1
        For i = k + 1 To n
            For j = k+1 To n + 1
                A(i, j) = A(i, j) - A(k, j) * A(i, k) / A(k, k)
            Next
        Next
    Next

    'حساب المجاهيل
    ReDim x(n) As Double: Dim s As Double
    For i = n To 1 Step -1
        s = 0
        For j = i + 1 To n
            s = s + A(i, j) * x(j)
        Next
        x(i) = (A(i, n + 1) - s) / A(i, i)
    Next
    EquationsGauss = x
End Function

تحسين البرنامج ومعالجة الأخطاء

قلنا أنه أحياناً يكون العنصر a(k,k) مساوياً للصفر لذلك لا يمكن التقسيم عليه، وقلنا أننا نبحث عن سطر i تحت السطر k يكون فيه a(i,k) لا يساوي الصفر، فإن وجد قمنا بالتبديل بين السطرين i و k وإلا نصدر رسالة خطأ تفيد بأن جملة المعادلات هذه لا يوجد لها حل وحيد.

إن عملية الاختبار هذه نضعها بعد السطر الذي يبدأ حلقة k وهذه العملية تتم كما يلي:

'اختبار العنصر المحور
If Abs(A(k, k)) <= 10 ^ -7 Then
    For i = k + 1 To n
        If Abs(A(i, k)) > 10 ^ -7 Then
            Dim tmp As Double
            For j = k To n + 1
                tmp = A(i, j): A(i, j) = A(k, j): A(k, j) = tmp
            Next
            Exit For
        End If
    Next
    If i = n + 1 Then Err.Raise 1000
End If

ندخل إلى حلقة تبديل الأسطر إذا كان العنصر a(k,k) يساوي الصفر أو أن القيمة المطلقة له أصغر من عدد صغير جداً نعتبره هو الصفر، لأنه في مثل هذه البرامج وبعد العديد من عمليات الضرب والقسمة والتقريب، فإنه لا يمكننا أن نثق أن ناتج العملية سيكون صفراً حتى لو كان على الورق بالحساب اليدوي هو صفر، بسبب كما قلنا التقريب بعد الفاصلة خاصة إذا كان عدد عمليات الضرب والقسمة كبيراً.

أيضاً نلاحظ أننا إذا وجدنا سطراً فيه a(i,k) لا يساوي الصفر نقوم بعملية التبديل، ثم نخرج من حلقة البحث i عن طريق الأمر Exit For، فإن لم نجد سيتم الخروج من الحلقة تلقائياً عندما تصل قيمة i إلى n+1 أي عندما تزيد عن الحد النهائي لها، وهكذا نختبر إن كانت قيمة i تساوي n+1 فإن جملة المعادلات لا تملك حلاً وحيداً لذلك نصدر رسالة خطأ رقمها 1000 مثلاً، عن طريق الأمر Err.Raise 1000

إن عملية التبديل تتم عن طريق تعريف متحول مؤقت tmp كما هو موضح أعلاه.

يصبح البرنامج النهائي كما يلي:

Public Function EquationsGauss(A() As Double) As Double()
    Dim n As Integer
    'عدد المعادلات
    n = UBound(A, 1)

    'إجراء عمليات التحويل
    Dim k As Integer, i As Integer, j As Integer
    For k = 1 To n - 1
        'اختبار العنصر المحور
        If Abs(A(k, k)) <= 10 ^ -7 Then
            For i = k + 1 To n
                If Abs(A(i, k)) > 10 ^ -7 Then
                    Dim tmp As Double
                    For j = k To n + 1
                        tmp = A(i, j): A(i, j) = A(k, j): A(k, j) = tmp
                    Next
                    Exit For
                End If
            Next
            If i = n + 1 Then Err.Raise 1000
        End If

        For i = k + 1 To n
            For j = k+1 To n + 1
                A(i, j) = A(i, j) - A(k, j) * A(i, k) / A(k, k)
            Next
        Next
    Next

    'حساب المجاهيل
    ReDim x(n) As Double: Dim s As Double
    For i = n To 1 Step -1
        s = 0
        For j = i + 1 To n
            s = s + A(i, j) * x(j)
        Next
        x(i) = (A(i, n + 1) - s) / A(i, i)
    Next
    EquationsGauss = x
End Function

ملاحظة هامة

في البرامج الإنشائية التي تعتمد على طريقة مصفوفة الصلابة (كالعناصر المحدودة) تكون مصفوفة الأمثال هي مصفوفة الصلابة، وشعاع الطرف الثاني هو شعاع الحمولات، والنتيجة هي الانتقالات.

لكن عادة تكون مصفوفة الصلابة كبيرة جداً ويؤدي هذا إلى استهلاك كبير للذاكرة، لذلك وجدت طرق لضغط مصفوفة الأمثال بالاستفادة من خصائص مصفوفة الصلابة، وهي التناظر، ووجود عناصر صفرية كثيرة.

فخاصية التناظر تتيح تخزين نصف المصفوفة تقريباً، ووجود عناصر صفرية كثيرة أيضاً يتيح لنا اختصار مساحة التخزين ويعتمد هذا على أسلوب ترقيم العقد.

يمكن الرجوع إلى المراجع المختصة للتعرف على طريقة الضغط هذه، وكيفية تعديل الخوارزمية التي درسناها هنا لتتوافق مع هذه الطريقة.

تطبيق البرنامج

كما قلت أعلاه فإن هذا البرنامج قد كتب بلغة Visual Basic 6 وحتى يتسنى لكل من تسول له نفسه ... أقصد لكل من أراد أن يجرب البرنامج ولم يكن عنده هذه اللغة، فقد قمت بوضع البرنامج ضمن ملف Excel أي كتبته باستخدام لغة Visual Basic for Application الخاصة بإكسل وهي نسخة مصغرة من لغة Visual Basic 6.

ومع هذا، فإن حل جملة معادلات خطية في إكسل عن طريق هذا البرنامج ليس ضرورياً، وقد أشرت إلى طريقة الحل في إكسل بالفيديو في الدرس الخامس.

إن البرنامج الذي كتبناه سابقاً هو عبارة عن تابع مغلق على نفسه، أي نقول بتمرير مصفوفة الأمثال الموسعة له، فيقوم بمعالجتها وإعادة شعاع قيم المجاهيل إن وجد أو يصدر رسالة خطأ.

ولاستخدامه نحتاج إلى إنشاء هذه المصفوفة، وطريقة إنشاء المصفوفة تختلف من برنامج إلى آخر.

ففي برامج طريقة الصلابة مثلاً، يقوم البرنامج بإنشاء مصفوفة الأمثال الموسعة (مصفوفة الصلابة مع الحمولات والمساند) بشكل تلقائي بناءً على نمذجة المستخدم.

أو ربما في برامج أخرى يكون الإدخال بشكل مباشر كما سنقوم الآن:

سنقوم في الخلية B2 من صفحة إكسل بإدخال عدد المعادلات، وسنقوم بإدخال مصفوفة الأمثال الموسعة ابتداءً من الخلية A3 ومن الضروري الالتزام بهذه الخلايا (إلا إذا قمنا بتعديل البرنامج).

راجع الشكل لمزيد من التوضيح.

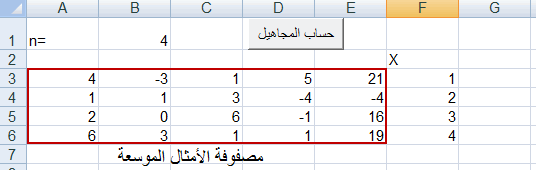
بالضغط على زر "حساب المجاهيل" يقوم البرنامج بحساب قيمة المجاهيل وعرضها في عمود مستقل بعد مصفوفة الأمثال.

أما البرنامج خلف هذا الزر فهو:

Sub Button1_Click()
    'قراءة مصفوفة الأمثال الموسعة
    Dim n As Integer
    n = Cells(1, 2)
    ReDim A(n, n + 1) As Double
    Dim i As Integer, j As Integer
    For i = 1 To n
        For j = 1 To n + 1
            A(i, j) = Cells(i + 2, j)
        Next
    Next

    For j = 1 To n + 1
        Cells(2, j) = ""
    Next
    Cells(2, n + 2) = "X"

    'إيجاد الحل
    On Error Resume Next
    Dim x() As Double
    x = EquationsGauss(A)

    If Err.Number = 0 Then 'اختبار وجود حل
        'إخراج الحل
        For i = 1 To n
            Cells(i + 2, n + 2) = x(i)
        Next
    Else
        MsgBox "لا يوجد حل وحيد لأن مصفوفة الأمثال شاذة"
    End If
End Sub

إن الأمر ReDim يقوم بتعريف أبعاد المصفوفة أو الشعاع.

أما السطر On Error Resume Next، فهو يخبر Visual Basic بأنه في حال حصول خطأ تابع إلى الخطوة التالية وخزن رقم الخطأ في الكائن Err.

لذلك نختبر الخاصية Value لهذا الكائن، فإن كانت صفراً، فإنه يوجد حل ويقوم بطباعته، وإلا فإنه يظهر رسالة تفيد بأنه لا يوجد حل.

انتهى بعون الله، وأرجو أن أكون قد وفقت في الشرح.

تحميل

• البرنامج السابق، ولكن لا تنس إذا قمت بفتحه أن تسمح لإكسل أن يقوم بتفعيل البرنامج أو الماكرو كما يسميه، وعملية التفعيل موضحة في الدرس الأول.